Simple vs. Compound Interest Definitions and Calculators
Interest is the extra money you pay when you borrow money from a lender. You have to pay back the amount you borrowed, plus interest. Interest is also the money you earn when you deposit and save your money in certain bank accounts.
Interest can be calculated as either simple interest or compound interest. This post will walk you through the difference between simple vs. compound interest and how they both work.
Simple vs. compound interest: essentials
Here’s the bottom line about simple vs. compound interest:
- If you deposit the same amount in different accounts
- And those accounts pay the same interest rate
- And you leave the accounts alone for the same amount of time
- Compound interest will give you more money
It works the other way too. Borrowing money costs more with compound interest than simple interest. Most credit cards charge compound interest.
Use a simple-interest or compound-interest calculator to make things easy, or read on to learn more about how simple interest and compound interest work.
Simple interest definition
Simple interest is calculated only on the principal, or original, amount of a loan.
Simple interest formula
Calculating simple interest is straightforward. You only need three things:
- Principal (P) — the amount you borrowed or deposited.
- Rate (R) — the interest rate per year. If it’s a percentage, you’ll need to divide by 100 to use it in the formula. (18% interest = 18/100 = 0.18 for the formula below.)
- Time (T) — the number of years you want to calculate the interest for.
For the formula, you just multiply them together:
Interest = P x R x T
For example, if you save $1000 in an account with a simple interest rate of 2%, you’ll earn $20 in interest after one year:
Interest = $1000 x 0.02 x 1 = $20
In fact, every year, you’ll earn exactly $20 in interest. After 2 years, you’ll have $40 in interest:
Interest = $1000 x 0.02 x 2 = $40
After 3 years, it’ll be $60, and so on.
On the flip side, if you borrow $1000 at a simple interest rate of 2%, you’ll owe $20 in interest every year.
Simple interest calculator
Want to see how your money adds up with simple interest? Plug your numbers into this easy simple-interest calculator.
Compound interest definition
Compound interest is calculated on the principal amount and any interest that has built up so far. This is true for both borrowing and depositing money.
In the real world, compound interest is very common in finance—such as in savings accounts at a bank or credit union, or for credit card balances.
In a savings account, you earn compound interest based on all the money that’s in the account, not just what you originally deposited. When you borrow money under compound interest, you pay interest on everything you owe, not just what you originally borrowed.
Compound interest formula
Calculating compound interest is more complex than calculating simple interest. Fortunately, a compound-interest calculator can make this easy.
For this formula, you’ll need:
- Principal (P) — the original amount borrowed or deposited.
- Rate (R) — the interest rate per year (remember to turn it into a decimal, just like we did before, so a rate of 18% would be 0.18 in the formula).
- Time (T) — the number of years.
- Number (N) — the number of times the interest compounds each year. (If it compounds once a month, N is 12 because there are 12 months in a year.)
Here’s the actual formula:
Interest = P x (1 + R / N)NT – P
If you save $1000 in an account with an interest rate of 2%, compounding once a year, you’ll earn $20 in interest after that first year (just as you would with simple interest):
Interest = $1000 x (1 + 0.02 / 1) 1 x 1– $1000 = $20
After year 2, however, your total interest earned will be $40.40 instead of $40:
Interest = $1000 x (1 + 0.02 / 1) 1 x 2 – $1000 = $40.40
After year 3, your total interest will be $61.21 instead of $60.
After year 4, your total interest will be $82.43 instead of $80, and so on.
The differences between simple vs. compound interest don’t seem very big at first, but over time, they can really add up.
Compound interest calculator
Want to see how your money adds up with compound interest? Plug your numbers into this easy compound-interest calculator.
Continuous compounding interest formula
Continuous compounding interest is what you get when you imagine breaking up the year even more—not into months or days, but into an infinite number of infinitely small time periods—and compounding your interest that often.
As theoretical as that sounds, there’s still a way to calculate it.
The more frequently interest is compounded, the more that interest adds up, assuming everything else stays the same. In other words, a bank account that paid 2% interest compounded daily would pay you more than one that paid 2% compounded monthly.
Interest that was compounded hourly would be higher, or compounded every minute would be higher than that, or every second … Right. You get it.
To figure out the interest on an account with continuous compounding interest, here’s the formula:
Interest = P x eRT – P
In this case, e is a mathematical constant, roughly equal to 2.7183. You can find e on any scientific calculator, or just use this continuously compounding interest calculator and plug in your numbers.
Simple interest vs. compound interest: which is better?
In a nutshell:
- Simple interest only pays interest on what you started with.
- Compound interest includes the interest you’ve earned and pays you interest on that too.
That’s why more time makes more of a difference. With simple interest, the amount you earn every interest “payday” never changes. With compound interest, you keep earning more each time.
And the frequency of that compounding matters too. The more often compound interest is calculated—yearly, quarterly, monthly, daily, or even continuously—the faster your interest payments rise.
Simple interest vs. compound interest examples:
Let’s say you decide to save $1000 in each of 3 accounts:
- Account 1 offers an annual simple interest rate of 2%.
- Account 2 offers the same 2% interest rate but compounds once a year.
- Account 3 also offers 2% interest, but it compounds monthly.
You can use the interest calculators linked above to see how these play out over time, or you can see how it plays out in the chart below, with a separate column for each account:
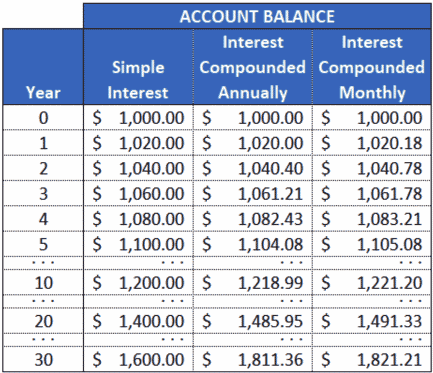
As you can see, the accounts with compound interest outpace the simple-interest account more and more over time. And the money that’s compounded monthly earns at a faster rate than the money that’s compounded annually.
Simple or compound interest on a loan: which is better?
Theoretically, when you borrow money, it’s better to pay simple interest than compound interest, but you don’t usually get to pick between the two.
Most loans—such as personal loans, car loans, student loans, and mortgages—are simple-interest loans. The main difference between them is the interest rate they charge, not how that interest is compounded.
Most credit cards, on the other hand, compound daily. Again, the main difference between credit cards is the interest rate they charge and what perks they offer (like cash back), not how their interest rate works.
Still, there’s one way you can choose between them: take control of your finances and start planning how and when you borrow money.
For example, if you buy a television on a credit card and pay it off over time, you’ll end up paying a lot more for that television than if you had paid cash. The interest on credit card debt compounds daily, and at a high interest rate!
On the other hand, if you save up for that television ahead of time, you can save a lot of money in interest. Plus, you’ll be in a better position to get a car loan, or any other kind of loan, if and when you need one, thanks to a lower debt-to-income ratio and higher credit score.
Simple interest vs. compound interest: wrap-up
Here’s the bottom line between simple interest and compound interest:
- When you’re getting interest, like in a savings account, compound interest is better—it pays more.
- When you’re paying interest, like when you borrow money, simple interest is better—it costs less.
But savings accounts almost always pay compound interest. And credit cards almost always charge compound interest. So you don’t usually get to pick between simple vs. compound interest.
That’s why the best way to manage your money is to think about the choices you do have, such as:
- Where you want to put your money—for example, putting some in a savings account as an emergency fund and investing the rest.
- How you want to borrow money—for example, deciding between a personal loan and a credit card.
- And how much you want to borrow, versus saving up ahead of time, or how quickly you want to pay off your debt.
The more you learn about your choices, and the better you are about tracking your finances, the better off you’ll be in the long run.
Quicken has made the material on this blog available for informational purposes only. Use of this website constitutes agreement to our Terms of Use and Privacy Policy. Quicken does not offer advisory or brokerage services, does not recommend the purchase or sale of any particular securities or other investments, and does not offer tax advice. For any such advice, please consult a professional.



